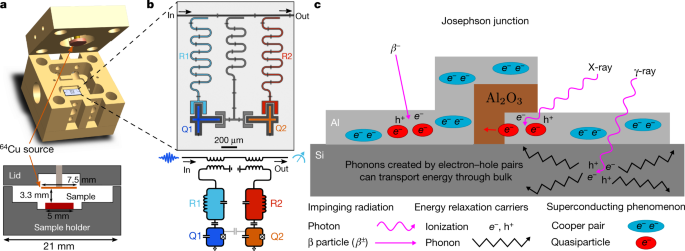
Measurement set-up

Extended Data Fig. 1a shows the measurement set-up used to measure the energy-relaxation times of the qubits. The qubit control pulses are created by a Keysight PXI arbitrary waveform generator. The in-phase and quadrature pulses are up-converted to the qubit transition frequency using single sideband IQ modulation. The readout pulses are created similarly. The control and readout pulses are combined and sent to the sample through a single microwave line. There is a total of 60 dB attenuation in the line to reduce the thermal noise from the room temperature and the upper stages of the dilution refrigerator. In the control line, there are absorbing filters (Eccosorb) before and after the sample, which further reduce the infrared radiation (thermal photons) reaching the qubit. The control line is inductively coupled to readout resonators R1 and R2.

The control pulses are applied to the qubit via the readout resonator, which filters the signal at the qubit frequency. Nonetheless, by using sufficiently large-amplitude pulses, the qubits can be excited in 25 ns.

The qubit state is determined using dispersive readout via a circuit quantum electrodynamics architecture⁴¹. The dispersive readout is based on the resonator frequency slightly changing depending on the state of the qubit. The change can be detected by using a single measurement tone near the resonator resonance frequency and measuring the transmitted signal in the microwave line. The measurement signal is boosted by a chain of amplifiers. The first amplifier used is a near-quantum-limited travelling-wave parametric amplifier (TWPA), which has a very low noise temperature and gain up to 30 dB (ref. ⁴²). As with all parametric amplifiers, the TWPA requires a pump tone, which is driven by a signal generator at room temperature. The measurement signal is further amplified by high-electron-mobility transistor (LNF) amplifier, which is thermally anchored to the 3 K stage of the refrigerator. At room temperature, there is a final pre-amplifier followed by a heterodyne detector. The down-converted in-phase and quadrature intermediate-frequency (IF) signals are digitized with a Keysight PXI digitizer (500 MHz sampling rate) and then further digitally demodulated using a field-programmable gate array integrated in the the digitizer to extract the measured qubit state. Measurement results are ensemble-averaged over many such trials to infer the occupation probability of the qubit being in a given state.

In the experiments, we used one sample with two transmon qubits, and a second sample with five transmon qubits. The qubits were fabricated using optical and electron-beam lithography. By construction, the structure of our qubits is kept simple and pristine—aluminium grown in a high-vacuum molecular beam epitaxy (MBE) chamber on top of high-resistivity silicon—to reduce defects that cause decoherence. The Josephson junctions have an additional layer of aluminium oxide in between the aluminium leads and are fabricated using double-angle shadow evaporation in another ultra-high-vacuum evaporator (different from the MBE). The fabrication is similar to that described in ref. ⁴³.

The table in Extended Data Fig. 1e shows the relevant qubit parameters. The reported energy-relaxation times are median values during the lead shield experiment. The values for the energy-relaxation rates of Q1 and Q2 differ from those reported for ⁶⁴Cu measurements because of their fluctuation over time.

Production of ⁶⁴Cu source

The ⁶⁴Cu radiation source was created by neutron activation of natural copper via the capture process ⁶³Cu(n,γ)⁶⁴Cu. Given its 12.7-h half-life, ⁶⁴Cu is well suited for deployment in a dilution refrigerator, since it takes 72–100 h to cool to base operating temperature. In the irradiation, we took into account the anticipated ⁶⁴Cu decay during the cool-down period, by specifically irradiating at higher levels of ⁶⁴Cu than used in the qubit study and then allowing the foils time to decay to lower levels of activity.

Two copper disks created from the same McMaster-Carr foil were irradiated with neutrons at the MIT Reactor (MITR). The two foils are referred to as sample A and A-Ref. The irradiated sample A was installed in the dilution refrigerator with the two qubits described in this study, while A-Ref was kept to determine the level of radioactive activation products. Each of the foils was 7.5 mm in diameter and 0.5 ± 0.1 mm thick. Samples A and A-Ref had a mass of 178.5 mg and 177.6 mg, respectively. The total neutron irradiation exposure was 7 min and 14 s in duration. With a high-purity γ-ray spectrometer, the A-Ref sample was used to determine the ⁶⁴Cu activation level. We determine the activity of sample A to be 162 ± 2 μCi at 9:00 a.m. ET, 13 May 2019. This activity is based on measurements of 1,346-keV γ-rays from ⁶⁴Cu using a high-purity germanium (HPGe) counter.

Despite the high copper purity (99.99%), trace elements with high neutron cross-sections can also be activated from the neutron irradiation process. The same HPGe counter was used to determine the presence of other trace elements, the results of which are reported in Extended Data Fig 6a.

Operation of NaI detector

A standard commercial NaI detector measures energy deposited in the NaI crystal through the scintillation light created when γ-rays or X-rays scatter atomic electrons in the crystal. The magnitude of the scintillation light signal, measured by a photomultiplier tube (PMT), is proportional to the energy deposited in the NaI crystal by the incident radiation. As the specific energy of γ-rays or X-rays are indicative of the radioactively decaying nucleus, an energy spectrum measured by the NaI detector can be used to determine the relative contributions of ionizing radiation in the laboratory due to different naturally occurring radioactive isotopes. In a normal laboratory environment, the dominant naturally occurring radioactive nuclei consist of isotopes in the uranium (²³⁸U) and thorium (²³²Th) decay chains as well as ⁴⁰K. These features are identified in Fig. 3a.

It is possible to reduce the high voltage applied to the PMT, effectively reducing the gain on the scintillation light signal from the NaI detector. This enables the measurement of ionizing cosmic rays—and the secondary radiation produced by them—as determined mainly by spectral features above 2.7 MeV (ref. ⁴⁴) (see Extended Data Fig 6e for the measured spectrum). We can fit the known spectrum of cosmic rays to the measured spectrum to find the cosmic-ray flux in the laboratory. The fit is shown in Extended Data Fig 6e. Note that, below 2.7 MeV, the large difference between the measurement and the fit is due to the radiation from nuclear decays, as shown in Fig. 3a.

Radiation transport simulations and normalization

To estimate the power density imparted into the qubits by radiation, we developed a radiation transport simulation. The simulation was performed with the Geant4 toolkit³¹ which is designed for modelling the interaction of radiation and particles with matter. The simulation geometry included a detailed model of the layers of the Leiden cryogenics CF-CS81 dilution refrigerator, the mounting fixtures and containment for the qubit, and the activated copper foil as it was located for the experiment. The qubit chip is modelled as a 380-μm-thick piece of silicon with a 200-nm aluminium cladding. Input power density is estimated by measuring simulated energy deposited into the aluminium layer. Three separate radiation source terms are considered: ⁶⁴Cu and the other isotopes in the activated copper foil; naturally occurring background radiation primarily from the concrete walls of the laboratory; and cosmic-ray muons.

To estimate the effect of isotopes in the copper, we make use of the radioactive decay simulation capabilities of Geant4. Instances of each isotope are distributed uniformly throughout the simulated foil volume. Geant4 samples the available decay modes for that isotope with appropriate branching fractions, and generates the corresponding secondary particles (γ-rays, β particles, positrons and so on), which are then tracked until they have deposited all their energy. By tallying these events, we can estimate the average input energy density into the qubit substrate per decay, or equivalently the average power density per unit of isotope activity. The total simulated spectrum at various times during the qubit measurement campaign are shown in Fig. 3b.

To understand the background levels of ionizing radiation present in the MIT laboratory where all qubit devices are operated, a 3″ × 3″ NaI scintillator detector was deployed near the dilution refrigerator where the qubit measurements were made. The detector was represented in the radiation transport simulation as a bare NaI cylinder (not including any housing, PMT and so on). γ-rays with an energy spectrum following the equilibrium emissions of the most common radioactive isotopes (²³⁸U, ²³²Th and ⁴⁰K) are simulated starting in a sphere surrounding the NaI detector with an isotropic initial direction. A small number of simulations were run with different-sized initial locations to evaluate the impact of this parameter, yielding a 10% systematic uncertainty.

To fit to the measured data, the simulated energy deposits must be broadened to account for the detector’s finite energy resolution. We used a quadratic energy-scaling function to map energy to measured analogue-to-digital converter counts, and a quadratic resolution function as a function of energy:

Each of the energy scale and resolution coefficients is left free in the fit, as well as the flux of each isotope, for a total of nine free parameters. The result for a fit over the range 0.2–2.9 MeV is shown in Fig. 3a. The fit is much better when performed over a narrower region of the data. This could be improved with a more sophisticated response function, but we address the issue by performing the fit separately over three energy ranges, 0.2–1.3 MeV, 1.3–2.9 MeV and 0.2–2.9 MeV, and taking the difference as a systematic uncertainty. This result is reported in the first line of the table in Extended Data Fig 6b. In total, the uncertainty in the fits contributes 8% to the systematic uncertainty. The simulated energy deposition efficiency for each external isotope is approximately equal to 0.04 keV s⁻¹ mm⁻³ per (cm⁻² s⁻¹), which yields a total power density from environmental γ-rays of 0.060 ± 0.005 keV s⁻¹ mm⁻³.

The same NaI detector, operated at lower gain, is used to estimate the cosmic-ray flux (see Extended Data Fig 6e). Cosmic-ray muons are simulated in a 1-m square plane above the detector, using the CRY package to generate the energy spectrum and angular distribution⁴⁵. The muon flux taken directly from CRY is 1.24 × 10⁻² cm⁻² s⁻¹. A fit to the low-gain NaI data, using the same convolutional technique as for γ-rays, yields (9.7 ± 0.1) × 10⁻³ cm⁻² s⁻¹, or about 20% lower than the CRY value. The same simulation gives an energy deposition efficiency in the qubits of 4.3 ± 0.2 keV s⁻¹ mm⁻³ per (cm⁻² s⁻¹) of cosmic-ray muon flux. This, in turn, yields a cosmic-ray-induced power density of 0.042 ± 0.002 keV s⁻¹ mm⁻³.

Throughout this work, we have based our analysis on the absorbed power density in the aluminium. However, radiation will also interact with and deposit energy in the silicon substrate. How much of this energy, if any, reaches the aluminium layer and is converted to quasiparticles is unknown, in part because we do not know the relevant coupling rates between silicon and aluminium or the various recombination rates of the quasiparticles. This motivated our use of a calibrated ⁶⁴Cu source, which we use to parameterize the net effect. In fact, as we show below, whether we consider aluminium only, or aluminium plus silicon, the difference in the net result changes by at most order unity. This counterintuitive result arises because the power densities in aluminium and silicon are approximately the same, and because the ⁶⁴Cu captures the net effect in either case.

Although ⁶⁴Cu captures the net effect well, small differences arise due to how the radiation is emitted and absorbed. For example, in comparison to highly penetrating radiation, ⁶⁴Cu deposits a larger fraction of its emitted energy into the aluminium, because a larger fraction is emitted as β particles. If the quasiparticle density is dominated by energy from the silicon rather than the aluminium, the relative strength of ⁶⁴Cu to the other trace activated isotopes would be approximately 60% lower. The external power density induced from environmental γ-rays is approximately 20% lower, whereas the cosmic-ray power density is 13% higher, for a net 7% total increase in external power. The lead shielding effectiveness (η) is also approximately 15% higher for the silicon than aluminium. By choosing aluminium, we are taking the most conservative estimate for the impact of environmental radiation on qubit energy relaxation.

We now show that these differences are at most an effect of order unity. If, for example, the quasiparticle generation rate is dominated by the total absorbed power in the silicon substrate, we can estimate the maximal relative error in the estimate of Γ₁ by comparing the ratios of the power densities of the external radiation P_ext absorbed in the aluminium film and the silicon substrate to the ratios of power densities induced by the ⁶⁴Cu source as

This would increase our estimate of the effect of the external radiation on the qubit energy-relaxation rate from (varGamma _1^(rmQ1),=,1/4,rmmrms^-1) to (varGamma _1^(rmQ1),=,asqrtomega _rmq^(rmQ1)P_rmermxrmt,f_rmcapprox 1/2.5,rmmrms^-1). See Supplementary Information for the derivation of the above formula. Note that the calculation is an upper-limit estimation, which would be reached only if the total phonon coupling between the silicon substrate and the aluminium were much stronger than the coupling between the sample and the sample holder.

Measurement of the qubit energy-relaxation rate

At the beginning of the measurement, all the qubits are initialized in their ground states. Owing to the finite temperature of their environment and hot quasiparticles^6,7, there is a small excited-state population, approximately 1.7% for these qubits and their qubit transition frequencies. This corresponds to an effective temperature T_eff ≈ 40 mK (ref. ⁶). At this temperature, the thermal quasiparticle population can be estimated to be

It is interesting to note that the quasiparticle density x_qp ≈ 7 × 10⁻⁹ due to environmental ionizing radiation (as inferred from our ⁶⁴Cu measurements) would correspond to an equilibrium quasiparticle temperature T ≈ 120 mK—consistent with the temperature below which qubit parameters such as T₁ stop following an equilibrium quasiparticle model in previous experiments (around 150 mK; see, for example, refs. ^7,40).

The qubit energy-relaxation rate Γ₁ is measured by first driving the qubits to their first excited state using a microwave π-pulse (see Extended Data Fig. 3b). The state of all the qubits is measured simultaneously after time t, which gives an estimate for their residual excited-state population p(t). By changing t, the time evolution of the populations can be determined. The model described in equation (2) in the main text can be fitted to the measured data to find the energy-relaxation rate Γ₁ of the qubits.

Estimating the internal radiation rate P
_int

An accurate estimate of the internal radiation rate P_int is important for comparing the feasibility of the shielding effect of the lead shield to the estimated effect of the external radiation power density on the change in qubit energy-relaxation rate δΓ extracted from the ⁶⁴Cu experiment. A simple way of making the estimate is to extract it from the fit to the data in Fig. 3c. However, the accuracy of the estimate is relatively low, as it is difficult to separate P_int from the energy-relaxation rate of the qubit due to sources other than quasiparticles, Γ_other. In principle, it is possible to distinguish the two sources, because according to equation (4), the scaling of Γ₁ is proportional to (sqrt{P_rmext+P_rmint+P_rmsrc}) whereas the internal energy-relaxation rate Γ_other contributes linearly to Γ₁ (see equation (2)). In practice, this is inaccurate, especially if quasiparticle loss is not the dominating loss-mechanism.

Instead, we use the shielding experiment to calculate an upper bound for P_int. In the limit of (P_rmintgg P_rmext), we can calculate an asymmetry parameter for the energy-relaxation times in the shield up or down positions,

where the index i refers to different rounds of the shield up/down experiment. The internal radiation rate P_int can be estimated using the experimentally measured median asymmetry parameter as

where (mathopPlimits^ sim _rmirmnrmt=P_rmirmnrmt+varGamma _rmormtrmhrmermr/(asqrtomega _rmq)) and (langle Arangle approx 0.0028) (see Extended Data Fig. 8). This gives the upper bound for P_int. Owing to the other relaxation mechanisms, the actual value of P_int is lower. For example, Γ_other = 1/200 μs⁻¹ would yield P_int ≈ 1.6 keV mm⁻³ s⁻¹ for the parameters of Q1. Here we emphasize that the estimate of the asymmetry parameter is based on the data gathered on all seven qubits used in the lead shield experiment, with all the qubits having different (fluctuating) values of Γ_other.

Efficiency of the lead shield

The reduction factor of external γ-radiation by the lead shield was evaluated using the radiation transport simulation described previously. In the simulation, γ-rays with energies drawn from the equilibrium emission spectra for ²³⁸U, ²³²Th and ⁴⁰K were generated isotropically from the surface of a sphere with 2.4 m diameter, centred on the qubits. The sphere completely enclosed the model for the lowered lead shield and the dilution refrigerator. The fraction of flux Φ reaching a smaller 17-cm-diameter sphere (fully inside the dilution refrigerator) was recorded. The table in Extended Data Fig. 6b shows the results for the no shield, shield down, and shield up, as well as the individual shield efficiency values (eta ^rmu,=,1-(varPhi ^rmu/varPhi ^rmnrmormsrmhrmirmermlrmd)) and (eta ^rmd,=,1-(varPhi ^rmd/varPhi ^rmnrmormsrmhrmirmermlrmd)).

A similar simulation was performed to calculate the efficiency of the lead shield against cosmic rays. As expected, the lead shield is ineffective at blocking cosmic rays, but works well against γ-rays originating from the nuclear decay events in the laboratory (see Extended Data Fig. 6c).

To validate the simulations, the NaI detector was operated separately inside the lead shield at the approximate location of the qubits in the shield-up configuration. This configuration was also simulated, and the output fitted to the measured spectrum using the same fit procedure as for the bare NaI. If the simulation and fit procedure are accurate, both fits should give the same values for the input flux. The results are reported in the first rows of the table in Extended Data Fig. 6b. The results for U and Th are consistent, whereas the values for K differ by about 2.5σ. It may be that the lead itself has a high level of ⁴⁰K, but we treat this as a systematic uncertainty, which is 7% of the total γ-ray flux.

Extended Data Fig. 1b–d shows a diagram of the lead shield and its dimensions.

Statistical analysis of the lead shield experiment

Since there are considerable fluctuations in the internal energy-relaxation rates Γ_other of the qubits, we performed a careful A/B test to verify that the effect of the lead shield on the qubit energy-relaxation time was not due to statistical error. In the measurement of the energy-relaxation rates of the qubits, there is uncertainty both due to the measurement accuracy and due to the fluctuations and drifts in the energy-relaxation rates over time. To reduce the uncertainty due to the measurement accuracy, we measured the energy-relaxation rates N times in each step of the A/B test. After N measurements the position of the lead shield was swapped (up versus down) and we performed another N measurements. This cycle was repeated 65 times with a sample containing qubits Q1 and Q2. To accelerate data acquisition, we installed a second sample with five qubits (Q3–Q7) and repeated the measurement cycle an additional 85 times. We used N = 50 for qubits Q1 and Q2, and N = 10 for qubits Q3–Q7 (see Extended Data Fig. 3a, c for the measured energy-relaxation rates). The median energy-relaxation times of the qubits are listed in the table in Extended Data Fig. 1e.

In the spirit of a Dicke radiometer experiment, performing repeated short measurement cycles was crucial for reducing the uncertainty in the relaxation rates due to drifts that occurred on timescales longer than the cycle period. The drift has been attributed in part to fluctuating two-level systems in dielectrics close to the qubit and in the junction region. However, by raising and lowering the shield often enough (every 50th measurement for qubits Q1 and Q2, and every 10th measurement for qubits Q3–Q7), the slow drift is mostly cancelled. Extended Data Fig. 3d shows the spectral density of the T₁ noise for qubits Q3, Q4, Q6 and Q7. The noise power density approximately follows a power law S = const/f^α with α ≈ 1.5. The fit to the model is shown with a solid orange line. The noise power density at the lead shield up/down cycle frequency of 1/(15 ± 1 min) is 3.4 × 10⁴ μs² Hz⁻¹. The noise power in the measurement can be estimated by integrating the spectral density over the noise bandwidth, which for the lock-in measurement yields 49 μs² (shaded red area in Extended Data Fig. 3d). If all the data were gathered sequentially, the noise power can be estimated to be 718 μs² (grey shaded are in Extended Data Fig. 3d), over an order of magnitude higher than in the Dicke experiment.

We used the median to estimate the net change δΓ₁ (between shield-up and shield-down configurations) to reduce sensitivity to individual measurement outliers. The quasiparticle contribution to the energy-relaxation rates of the qubits depends on their frequencies according to equation (5), and therefore we have normalized the changes in the energy-relaxation rates to the frequency of Q1 by multiplying by a conversion factor (sqrt{omega _rmq^(rmQmathrm1)/omega _{rmq}^(rmQi)}).

We neglected a small percentage of the total data points where (varGamma _1^rmu) or (varGamma _1^{rmd}) was less than 1/30 μs⁻¹ or their difference was more than 10 standard deviations of all the measured differences, as these tended to indicate suspect rates derived from poorly resolved decay functions. We then calculated the 95% CIs for δΓ₁ using the normal approximation for the CI of the sample median⁴⁶.

We applied the Wilcoxon signed-rank test to determine whether the median of the two distributions (corresponding to the shield-up versus shield-down configurations) differed in a statistically significant manner. This is a non-parametric test and can be used for data that are not normally distributed. For δΓ₁, the single-sided Wilcoxon signed-rank test gives a P-value of P = 0.006 for the null hypothesis that the median of the energy-relaxation rates with the shield is the same or higher than without the shield. The test statistic w ≈ 25,000,000 with a sample size of 9,846. For (Pll 0.05), we can reject this null hypothesis and conclude that the shield reduces the energy-relaxation rate.

We performed several tests to verify the correctness of our statistical analysis. First, we checked that the result is not sensitive to the post-processing that we performed on the data. The first panel of Extended Data Fig. 7a shows the P-value of the Wilcoxon signed-rank test for a range of different cut-off parameters. The P-value remains low for all the realistic parameters we tested, verifying that the finding is not an artefact of post-processing or parameter selection. The median value is even less sensitive to the post-processing, shown in the lower-left panel. The blue diamond in the upper-left corner shows the point where no post-processing is done. The blue circle shows the values that we use in the main text, (T_1^{rmcrmurmt-rmormfrmf},=,30,rmmu rms) and (n_sigma ^rmcut-rmoff,=,10).

Next, we tried shuffling the data by comparing the energy-relaxation rates of the measurements to the next measurement without moving the shield. In this case, we would expect the signal to vanish completely, and the null hypothesis to be manifestly true. The result is shown in the middle column of Extended Data Fig. 7a. In this case, the P-value is close to 1, which implies that we must accept the null hypothesis that there is no signal if we do not move the shield, as expected.

In the third test, we completely randomized the pairs of measurements that we compared, resulting in overall high P-value, supporting our analysis (third column).

Extended Data Fig. 7b shows a section of Extended Data Fig. 7a along the dashed lines in the left and middle panels. The shaded areas show the 68% CI of the medians.